- Версия(и) Minecraft
- 1.18.2+
Всем привет!
Я надеюсь, что все уже знакомы с первой статьёй. Если нет, советую ознакомиться, иначе многое описанное далее будет вам не понятно.
Рассказывать буду на примере версии 1.18.2, так как с ней я работал больше всего. Материала получилось много, так что запаситесь терпением и переключите мозг в режим приёма информации.
Итак, поехали!
Запомним эту информацию, мы к ней ещё вернёмся. А теперь перейдём к самой статье.
Итак, задача: разнообразить ландшафт.
Первая проблема, с которой мы столкнёмся – это как сообщить генератору, где именно должен находится тот или иной элемент. Но, если немножко подумать, станет ясно, что это вовсе не является проблемой: например, для распределения биомов в версиях до 1.18 были придуманы слои, и они весьма неплохо справлялись с созданием 2D карт. Можно использовать их для своих целей. Можно вычислять положение элемента исходя из координат местности. А можно использовать для создания карты те же самые шумы.
Применение шумов для генерации как местности, так и её деталей, оказалось весьма удобным и элегантным решением. К примеру, лапшичные пещеры генерируются на основе четырёх шумов различного масштаба. Но о них чуть позже. Пока я постараюсь объяснить, как работать с единичным шумом.
Кстати, я тут недавно осознал, что трёхмерный шум значений – это, на самом деле, четырёхмерная штука. Приятно осознавать, что мы будем учиться работать с четырёхмерным объектом
Рассмотрим простой пример. В качестве основы возьмём чистый градиент и смешаем его с шумом, но не так, как мы делали это в первой статье, а используя следующую формулу для вычисления веса вершины:
Вот, что получаем в итоге. Здесь видно, что особенность ландшафта, а именно пещера, появилась только в определённом месте. При этом остальной ландшафт остался нетронутым. Как все уже догадались, мы использовали шум в качестве карты.

Но постойте! Почему всё такое рубленное?
Дело в том, что разница между модулями весов соседних точек получилась слишком велика. Как мы помним из предыдущей статьи, значения градиента сверху и снизу могут быть весьма большими. При этом в качестве целевого значения для нашей пещеры мы всегда возвращаем

Вот так уже лучше. Всё плавно и красиво. Но выглядит как-то иначе. В прошлый раз пещера начиналась сразу же на обозначенной нами границе в
Дело в том, что шум весьма непредсказуемая вещь. Он случаен, и в этом его смысл. И если границу, соответствующую значению
Попробуем ещё раз изменить формулу, но вместо постоянного значения

Вот это уже больше похоже на первый вариант. Мы вынудили нулевую поверхность весов сместится туда, где она была раньше. Однако на поверхности граница пещеры выглядит слишком резкой. Это происходит из-за того, что веса внутри пещеры и за её пределами одинаковые, и они с равной силой «давят» на контур.
Попробуем нарушить это равновесие. Например, следующим способом:

Такой результат нас вполне устраивает. Мы видим, как значения точек внутри пещеры стали сильнее, чем значения точек вовне.
Можно было бы применить иную формулу, например такую:
Это так же нарушило бы равновесие весов, но имело бы немного другой результат. В процессе лепки ландшафта нет конкретных решений. Всё это зависит от вас и вашей фантазии.
Можно было бы шагнуть ещё дальше и использовать один шум как карту для второго. Например так:

Мы видим, как ландшафт сформировался везде, кроме того места, где когда-то была пещера. Получилась своего рода равнина. Хотя края у неё и не особо плавные. Нечто подобное мы наблюдали в самом начале, когда разница между весами соседних вершин была слишком большой.
Да эффект похож, но причина немного иная. В данном случае нулевая отметка градиента располагается как раз на границе между блоками, на высоте 128. При интерполяции вблизи этой отметки получаются очень маленькие величины. Маленькие, но всё-таки не нулевые. Так как блоки мы располагаем при любом весе, который больше нуля, генератор ставит в этих местах по полному блоку. Отсюда и получаются такие зазубрены, равные по размеру сетке чанка.
Как с этим справится? Очень легко! Позвольте себе немного хаоса. Измените слегка высоту градиента, чтобы убрать нулевое значение с границы блока. Сделайте его не
Если для вас это слишком большая жертва, измените это значение при интерполяции:
Это уже не выглядит настолько страшным, зато результат станет намного симпатичнее.

Хотите иметь вместо равнины впадину? Нет проблем! Опустите градиент не на

Вуаля! Красивая ровная впадина готова!
Хотите не впадину, а гору? Вы уже знаете, что делать
К слову, если для некоторых количество хаоса в коде перешло все границы, спешу вас успокоить: в большинстве случаев оперировать «кривыми» цифрами не придётся. Скорее всего в вашем чанке будет намешено столько карт, шумов и градиентов, что они даже против вашей воли внесут необходимый для генерации хаос. Вручную это придётся делать только там, где ландшафт будет плавно переходить в какие-то ровные поверхности, как это было на примере выше. Но это будут единичные случаи.
Итак, мы рассмотрели простейшие примеры смешивания шумов и градиентов, использования карт и т.д. Даже успели увидеть некоторые глюки и узнали, как с ними бороться. Теперь давайте поговорим о недостатках такого подхода. И основной из них – детализация.
И да, можно психануть, и уменьшить сетку чанка до размера в один блок, но при этом количество вычислений вырастет в разы, а если быть точным, в 4 х 4 х 8 = 128 раз. Нам бы этого не хотелось.
Чтобы чётче понять проблему детализации, давайте рассмотрим простой пример. Предположим, что мы ходим сгенерировать под землёй узкую пещеру, как на скриншоте.
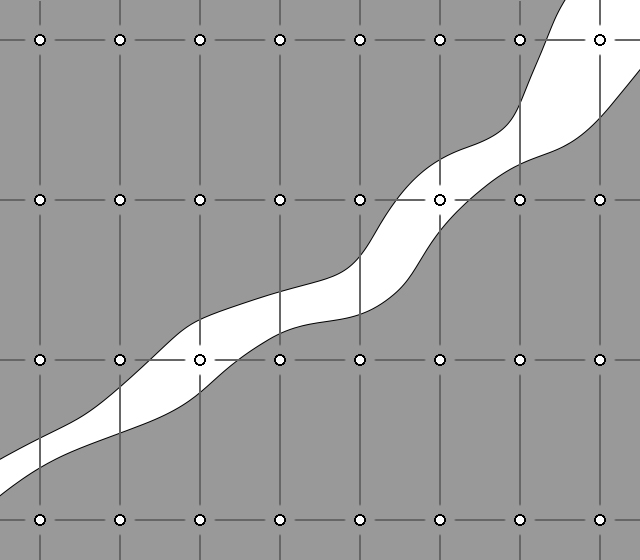
Здесь серым показан камень, а белым – воздух самой пещеры.
Допустим, что мы какими-то сложными вычислениями расставили по нужным местам необходимые нам веса сетки чанка. Красные – положительные, синие – отрицательные.
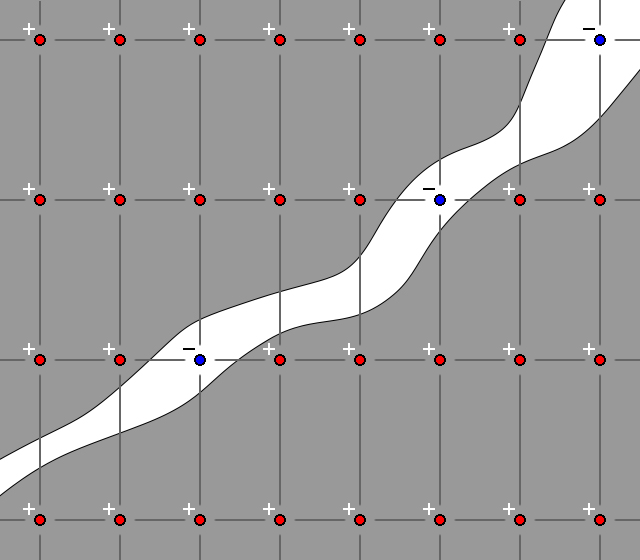
Вроде, всё выглядит правильно, и пещера должна получится отличной! Но не забывайте, что финальный ландшафт будет рассчитываться путём интерполяции.
Как наша пещера выглядит для генератора? Примерно вот так. Тёмное – положительное, светлое – отрицательное.

По итогу, после расставления всех блоков, мы получим следующий результат.
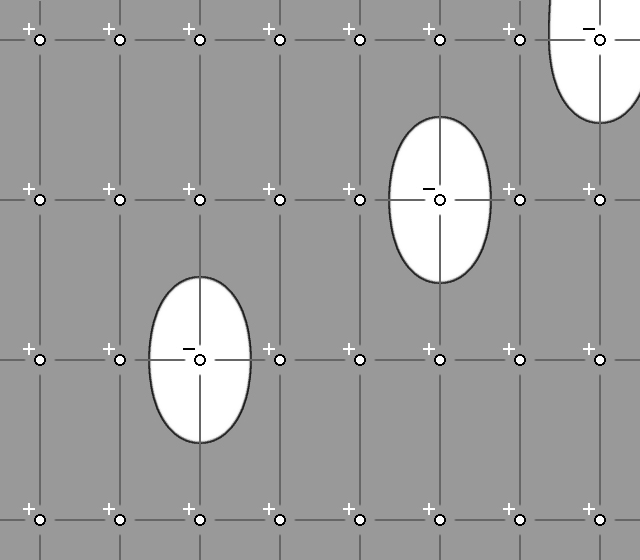
Это не сильно напоминает пещеру.
Из ванильного кода видно, что с данной проблемой столкнулись и разработчики игры. Но не зря же они целый год (по их словам) писали свой генератор. В итоге, они придумали довольно интересное решение: если нельзя получить детальный ландшафт на одном «интерполируемом пространстве», значит нужно добавить к нему второе.
Что будет, если создать ещё одно подобное пространство? Для каждого конкретного блока в финале мы получим не один, а два веса. Или три. Всё зависит от количества добавляемых пространств. На самом деле, в ванильном генераторе их можно создавать сколько угодно, подобно слоям в фотошопе.
Да, к такому нас жизнь не готовила
И если реально рассматривать трёхмерные шумы как четырёхмерный объект, то с добавлением новых пространств, мы уходим чуть ли не в пятое измерение. Свихнуться можно.
Но, если понять основные принципы и законы построения, это перестанет быть настолько пугающим.
Теперь давайте по порядку. Вернёмся к нашей пещере, но будем использовать не одно, а два пространства. Распределим веса в этих пространствах следующим образом. На первом пространстве все положительные значения будут располагаться с одной стороны пещеры, а на втором – с другой. При этом нужно следить, чтобы на обоих пространствах внутри пещеры веса сохраняли отрицательные значения. Выглядеть это будет примерно так.
После интерполяции получим следующую картину.

В финале, в каждом блоке мы имеем по два веса. При этом, внутри пещеры оба эти веса отрицательные. Теперь нам остаётся только поставить блоки там, где хотя бы один из весов положительный. Если разговаривать языком формул, то выглядеть это будет так:
После данных вычислений схема весов приобретёт следующий вид.

Ну а финальная картина будет такой.
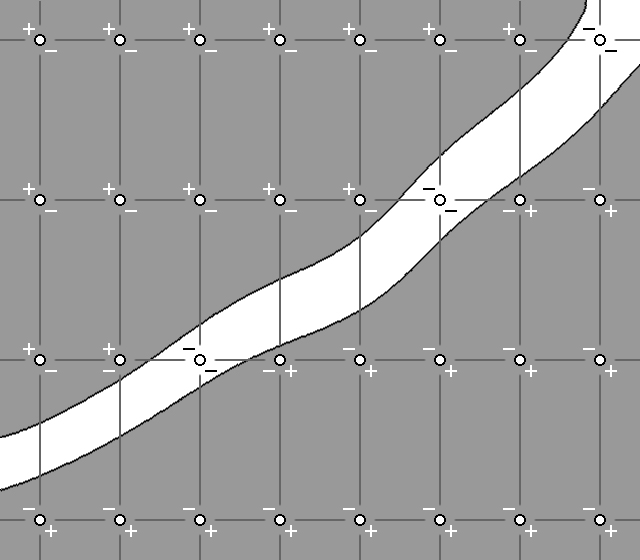
Таким образом мы получили особенность ландшафта, которая меньше сетки чанка. Количество вычислений при этом увеличилось всего в 2 раза.
Да, конечно, мы видим, что финальная пещера не в точности повторяет наши хотелки, она более сглаженная и не такая интересная. Но мы всегда можем смешать её с ещё одним шумом, чтобы получить некоторые флуктуации.
Играясь с несколькими интерполируемыми пространствами, мы реально можем лепить из ландшафта то, что нам хочется. Главное, это разработать алгоритм получения той или иной формы. И это опять зависит только от вас и вашей фантазии. Я же, со своей стороны, могу лишь привести ещё один пример элегантного решения, и примером этим будут: ванильные лапшичные пещеры.
Как говорила Алиса: «С одной стороны чего? И с другой стороны чего?!»
На самом деле, если бы мы сгенерировали приведённый мною пример, то получили бы вовсе не пещеру, а широченный наклонный холл с низким потолком. На одном из пространств положительные веса располагались бы над этим холлом, а на втором – под ним.
Чтобы ограничить его и по ширине, пришлось бы использовать ещё два пространства. Это усложнило бы процесс. Но есть способ хитрее: ванильный генератор предполагает разделение сложных и не сложных вычислений. К примеру, вычисление веса какой-либо из точек чанка может быть довольно сложным, так как оно завязано на положение этой точки в пространстве, сочетание различных шумов, градиентов и их преобразованиях. С другой стороны, выяснение ставить ли блок на месте положительного веса происходит очень даже легко. Там всего одно условие.
Как вы догадались, сложные вычисления выполняются только для точек решётки чанка, а простые мы можем себе позволить считать для каждого блока.
Ну и раз уж они такие простые, так почему бы и не добавить к ним ещё несколько несложных преобразований? Например, таких:
После применения данной формулы мы получим из этой картинки:

Эту:

Что-то похожее мы уже видели, правда?
Да, как вы догадались, я сформировал узкую пещеру (в вертикальном сечении) на основе единственного интерполируемого пространства, лишь слегка поработав с финальным весом блока. Второе же пространство можно использовать для ограничения этой пещеры по ширине, то есть в горизонтальном сечении.
Как это получилось?
Следующие схемы в полной мере ответят на данный вопрос.
На предыдущих картинках я показывал сечение чанка, чтобы градиент весов или трёхмерный шум можно было увидеть нашим двухмерным зрением. Теперь пойдём ещё дальше и сделаем сечение по сечению, представим градиент в виде графика
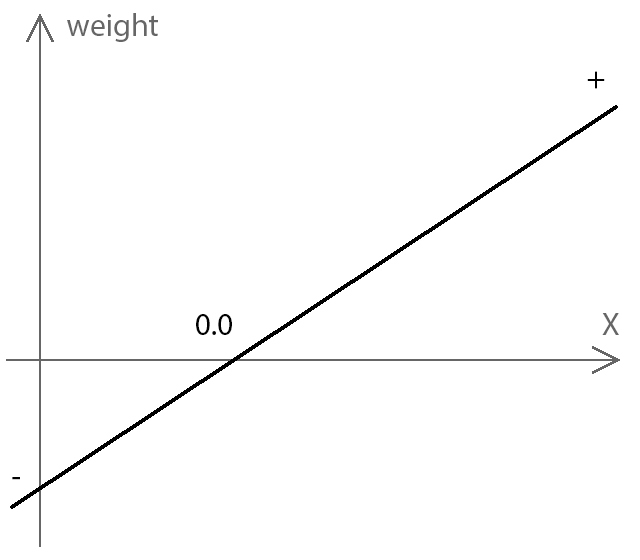
Теперь вычислим модуль градиента, то есть все отрицательные значения сделаем положительными. Иными словами, отзеркалим график относительно нулевой отметки.
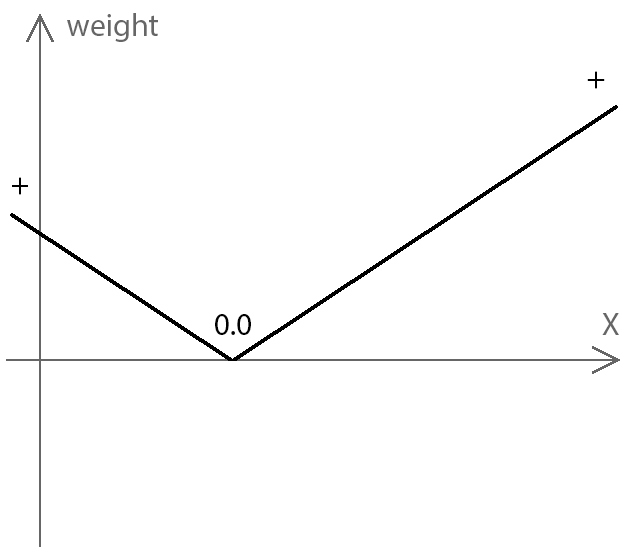
Ну и следующий шаг: опустим график на
Таким образом, в месте, где градиент пересекал нулевую отметку, мы получили узкую полоску отрицательных значение. Всё остальное поле стало положительным.
Думаю, теперь вам стал понятен смыл описанной выше формулы.
Ну а сейчас настало время включить на полную своё пространственное воображение и погрузиться с головой в создание «лапшичных» пещер. На этот раз работать мы будем не с градиентом, а с трёхмерным шумом, но над ним мы будем производить примерно те же манипуляции, что были описаны ранее.
Помните, в первой статье я показывал скриншот генерации, на основе чистого шума значений? Ландшафт на нём напоминал трёхмерную губку. Её форма в точности повторяла поверхность нулевых значений в шуме. Ровно таких же нулевых значений, с которыми мы уже работали в примере с градиентом. Это значит, что и к интерполированным значениям трёхмерного шума можно применить ту же самую формулу, что мы применяли к градиенту. Но результатом будет не низкий и широкий холл, а кое-что гораздо более сложное. У нулевой поверхности шума появится толщина! Изнутри это будет выглядеть примерно так.

Если вы способны понять, что здесь происходит, браво! Значит я не зря писал эту статью.
Если это всё-таки трудновато, то вот вам сечение по шуму и результат применения формулы.
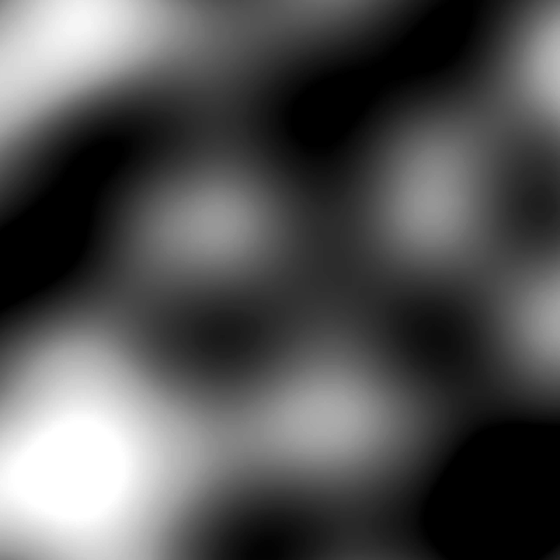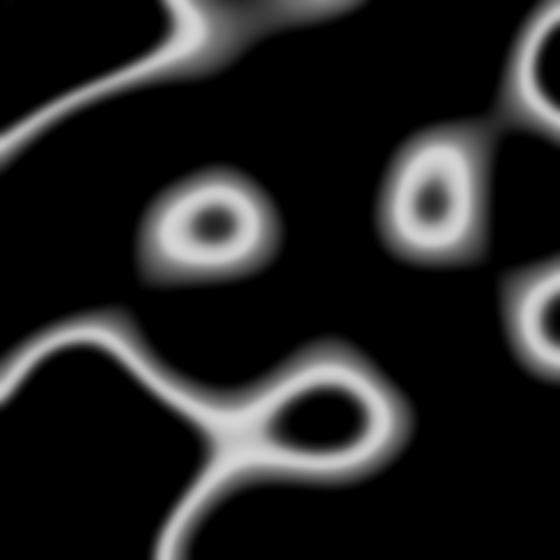
Ну а если всё ещё не понятно, то вот вам и сечение по сечению шума и последовательность его преобразований.
Так уже понятнее, правда? Но, уверяю вас, это ещё не самое страшное. Здесь мы получили только одно интерполируемое пространство, которое, подобно примеру с градиентом, ограничивает наши будущие пещеры только с двух сторон, «сверху» и «снизу». Если такие понятия вообще применимы к предыдущему скриншоту. Теперь нам нужно добавить сюда ещё одно пространство с шумом. Только второй шум должен чем-то отличаться от первого, например размером или сидом.
Что происходит далее? Правильно! Мы пересекаем одно пространство со вторым так, как это делали ранее, используя формулу:
К сожалению, тут моя способность подготавливать простые схемы достигает своего предела возможностей. Результаты данного преобразования можно увидеть только самому в игре. Но, я думаю, что каждый уже успел с ними ознакомиться 
Ах да! В середине статьи я упоминал, что для создания лапшичных пещер используются четыре шума. Два из них я описал, а ещё два выполняют функцию деформирования. По первому шуму определяют толщину пещеры, то есть то число, которое вычитается из модуля весов. Второй же шум определяет само место размещения данных пещер, чтобы они встречались не во всём подземном мире, а лишь в некоторых местах (смотри самый первый пример с использованием шума, в качестве карты).
В коде игры это выглядит так:
На этом всё! Статья получилась объёмной и развёрнутой. Не ожидал, что данная тема выльется в такое количество материала. Тем, кто выдержал всё это, спасибо за прочтение. Надеюсь, вы сможете применить полученную информацию на практике 
Напоследок, вот вам несколько скриншотов из Туманного мира




Прошло немало времени с момента написания первой статьи, на пороге уже версия 1.20, несколько раз разработчики успели переписать генератор чанков, производство Туманного мира всё ещё не закончено, но и не заброшено. И да, я до сих пор занят полировкой собственного генератор, хоть и основанного на ванильном, но и во многом отличающегося от него, заточенного специально под особенности создаваемого мной мира.
И вот, после всех мытарств с кодом, изучения ванильного генератора и попыток запихнуть в свой всё необходимое, я кое-что осознал. Не смотря на большие изменения в коде, основные принципы построения поверхности и её детализации остаются неизменными. Всё, что меняется от версии к версии, относятся лишь к удобству использования этих самых принципов и к их контролю.
Не хочу сказать, что среди нововведений нет интересных решений, но об этом чуть позже.
Это я всё к чему? А к тому, что со времён первого тутора у меня накопилось достаточно материала чтобы написать ещё пару статей. В них я хотел бы не просто рассказать, как работает ванильный генератор, но и попытаться объяснить те самые принципы, лежащие в его основе, чтобы вы сами могли оперировать ими, лепить ландшафт так, как вам захочется и, возможно, написать свой собственный генератор
И вот, после всех мытарств с кодом, изучения ванильного генератора и попыток запихнуть в свой всё необходимое, я кое-что осознал. Не смотря на большие изменения в коде, основные принципы построения поверхности и её детализации остаются неизменными. Всё, что меняется от версии к версии, относятся лишь к удобству использования этих самых принципов и к их контролю.
Не хочу сказать, что среди нововведений нет интересных решений, но об этом чуть позже.
Это я всё к чему? А к тому, что со времён первого тутора у меня накопилось достаточно материала чтобы написать ещё пару статей. В них я хотел бы не просто рассказать, как работает ванильный генератор, но и попытаться объяснить те самые принципы, лежащие в его основе, чтобы вы сами могли оперировать ими, лепить ландшафт так, как вам захочется и, возможно, написать свой собственный генератор
Рассказывать буду на примере версии 1.18.2, так как с ней я работал больше всего. Материала получилось много, так что запаситесь терпением и переключите мозг в режим приёма информации.
Итак, поехали!
Углубимся в тайну
Для начала хотел бы заполнить один пробел из предыдущей статьи, а именно, объяснить магию, которая происходит в методеdoFill(). Это тот самый метод, где из 8-ми вершин сетки чанка собирается финальный кусок ландшафта. Так вот происходит там ни что иное, как интерполяция. Всего-навсего. Только интерполяция эта трёхмерная. Сперва интерполируются 4 пары точек по вертикали (ось Y), затем две пары по оси X, и, наконец, оставшаяся одна пара по Z. В финале мы получаем значение веса для конкретного блока внутри ячейки чанка.Запомним эту информацию, мы к ней ещё вернёмся. А теперь перейдём к самой статье.
Работа с шумами
Описанный в первой статье механизм даёт большие возможности. С его помощью можно сформировать и горы, и равнины. Однако, если использовать только смесь шума с градиентом, мир получится весьма однообразным. А ведь нам всем хочется добавить в него изюминку, чтобы игрок время от времени находил какие-нибудь необычные природные образования. С одной стороны, сами биомы с различной высотой и величиной перепада рельефа – это уже попытка разнообразить ландшафт. Но не стоит ограничивать себя только ими.Итак, задача: разнообразить ландшафт.
Первая проблема, с которой мы столкнёмся – это как сообщить генератору, где именно должен находится тот или иной элемент. Но, если немножко подумать, станет ясно, что это вовсе не является проблемой: например, для распределения биомов в версиях до 1.18 были придуманы слои, и они весьма неплохо справлялись с созданием 2D карт. Можно использовать их для своих целей. Можно вычислять положение элемента исходя из координат местности. А можно использовать для создания карты те же самые шумы.
Собственно, так и было сделано в более поздних версиях. Биомы сейчас определяются на основе 6-ти параметров, вычисленных в классе
Начиная с версии 1.18 больше нет жёсткой связи ландшафта с биомом. Сейчас ландшафт и биомы генерируются параллельно и зависят от параметров климата. Поэтому пока забудем про биомы как таковые. Да и про сам климат тоже. Как я писал выше, это лишь оптимизация работы с базовыми механизмами генерации. А ведь нам нужно понять именно их.
Climate: температура, влажность, континентальность, эрозия, высота и странность. Многие из этих параметров сгенерированы на основе шумов.Начиная с версии 1.18 больше нет жёсткой связи ландшафта с биомом. Сейчас ландшафт и биомы генерируются параллельно и зависят от параметров климата. Поэтому пока забудем про биомы как таковые. Да и про сам климат тоже. Как я писал выше, это лишь оптимизация работы с базовыми механизмами генерации. А ведь нам нужно понять именно их.
Применение шумов для генерации как местности, так и её деталей, оказалось весьма удобным и элегантным решением. К примеру, лапшичные пещеры генерируются на основе четырёх шумов различного масштаба. Но о них чуть позже. Пока я постараюсь объяснить, как работать с единичным шумом.
Кстати, я тут недавно осознал, что трёхмерный шум значений – это, на самом деле, четырёхмерная штука. Приятно осознавать, что мы будем учиться работать с четырёхмерным объектом
Рассмотрим простой пример. В качестве основы возьмём чистый градиент и смешаем его с шумом, но не так, как мы делали это в первой статье, а используя следующую формулу для вычисления веса вершины:
Java:
public double getWeight(int x, int y, int z) {
double noise = this.noise.getValue(x, y, z); // Генерируем произвольный шум
if (noise > 0.5) return -1; // Фильтруем значение финального веса по значению шума. Возвращаем -1 (пустоту) только тогда, когда значение шума больше 0.5. Таким образом новый вес будет применён не ко всему ландшафту, а только некоторым его местам.
return (128.0 - y) / 16; // Во всех остальных случаях возвращаем чистый градиент с нужными нам высотой и контрастом
}Вот, что получаем в итоге. Здесь видно, что особенность ландшафта, а именно пещера, появилась только в определённом месте. При этом остальной ландшафт остался нетронутым. Как все уже догадались, мы использовали шум в качестве карты.
Но постойте! Почему всё такое рубленное?
Дело в том, что разница между модулями весов соседних точек получилась слишком велика. Как мы помним из предыдущей статьи, значения градиента сверху и снизу могут быть весьма большими. При этом в качестве целевого значения для нашей пещеры мы всегда возвращаем
-1. Получается, что при интерполяции большой вес точки с положительным значением как бы придавливает нулевую отметку к стенке ячейки чанка, так как соседняя, отрицательная точка не может этому сопротивляться. В итоге мы получаем что-то больше похожее на каменоломню. Нам этого не надо. Сделаем распределение весов более плавным:
Java:
public double getWeight(int x, int y, int z) {
double gradient = (128.0 - y) / 16; // Создаём чистый градиент
double noise = this.noise.getValue(x, y, z); // Генерируем произвольный шум
if (noise > 0.5) { // Фильтруем по значению шума
noise = (noise - 0.5) * 2; // Приводим отфильтрованные значения шума к формату 0 … 1
gradient = Mth.lerp(noise, gradient, -1); // Интерполируем между весом в градиенте и -1 с использованием нового формата шума
}
return gradient;
}Вот так уже лучше. Всё плавно и красиво. Но выглядит как-то иначе. В прошлый раз пещера начиналась сразу же на обозначенной нами границе в
0.5.Дело в том, что шум весьма непредсказуемая вещь. Он случаен, и в этом его смысл. И если границу, соответствующую значению
0.5 мы увидели на предыдущем скриншоте, то сейчас стало очевидно, что за этой границей нет значений, превышающих 0.75. Это означает, что интерполяцией нам не получить отрицательных весов внутри пещеры. Такое бывает, с этим просто нужно смириться.Попробуем ещё раз изменить формулу, но вместо постоянного значения
-1, противопоставим градиенту его противоположность:
Java:
public double getWeight(int x, int y, int z) {
double gradient = (128.0 - y) / 16;
double noise = this.noise.getValue(x, y, z);
if (noise > 0.5) {
noise = (noise - 0.5) * 2;
gradient = Mth.lerp(noise, gradient, Math.min(-gradient, 0.0)); // Возвращаем не -1, а инвертированное значение веса градиента. Но не даём ему уйти в плюс! Иначе вместо пещеры мы получим гору.
}
return gradient;
}Вот это уже больше похоже на первый вариант. Мы вынудили нулевую поверхность весов сместится туда, где она была раньше. Однако на поверхности граница пещеры выглядит слишком резкой. Это происходит из-за того, что веса внутри пещеры и за её пределами одинаковые, и они с равной силой «давят» на контур.
Попробуем нарушить это равновесие. Например, следующим способом:
Java:
public double getWeight(int x, int y, int z) {
double gradient = (128.0 - y) / 16;
double noise = this.noise.getValue(x, y, z);
if (noise > 0.5) {
noise = (noise - 0.5) * 2;
gradient = Mth.lerp(noise, gradient, Math.min(-gradient, -1.0)); // Не даём нашему инвертированному градиенту уйти не просто в плюс, а обрубаем у него все значения выше -1.0.
}
return gradient;
}Такой результат нас вполне устраивает. Мы видим, как значения точек внутри пещеры стали сильнее, чем значения точек вовне.
Можно было бы применить иную формулу, например такую:
Math.min(-gradient – 1.0, 0.0)Это так же нарушило бы равновесие весов, но имело бы немного другой результат. В процессе лепки ландшафта нет конкретных решений. Всё это зависит от вас и вашей фантазии.
Можно было бы шагнуть ещё дальше и использовать один шум как карту для второго. Например так:
Java:
public double getWeight(int x, int y, int z) {
double gradient = (128.0 - y) / 16; // Создаём чистый градиент
double noise = this.noise.getValue(x, y, z); // Генерируем шум, который будем использовать в качестве карты
double terrainNoise = this.terrainNoise.getValue(x, y, z); // Генерируем второй шум, который будем смешивать с градиентом используя нашу карту
noise = Mth.clamp(noise * 2, 0.0, 1.0); // Модифицируем карту так как нам надо
gradient = Mth.lerp(noise, gradient + terrainNoise, gradient); // Смешиваем
return gradient;
}Мы видим, как ландшафт сформировался везде, кроме того места, где когда-то была пещера. Получилась своего рода равнина. Хотя края у неё и не особо плавные. Нечто подобное мы наблюдали в самом начале, когда разница между весами соседних вершин была слишком большой.
Да эффект похож, но причина немного иная. В данном случае нулевая отметка градиента располагается как раз на границе между блоками, на высоте 128. При интерполяции вблизи этой отметки получаются очень маленькие величины. Маленькие, но всё-таки не нулевые. Так как блоки мы располагаем при любом весе, который больше нуля, генератор ставит в этих местах по полному блоку. Отсюда и получаются такие зазубрены, равные по размеру сетке чанка.
Как с этим справится? Очень легко! Позвольте себе немного хаоса. Измените слегка высоту градиента, чтобы убрать нулевое значение с границы блока. Сделайте его не
128, а 127.99.Если для вас это слишком большая жертва, измените это значение при интерполяции:
Java:
gradient = Mth.lerp(noise, gradient + terrainNoise, gradient - 0.01);Хотите иметь вместо равнины впадину? Нет проблем! Опустите градиент не на
0.01, а больше:
Java:
gradient = Mth.lerp(noise, gradient + terrainNoise, gradient - 0.56);Вуаля! Красивая ровная впадина готова!
Хотите не впадину, а гору? Вы уже знаете, что делать
К слову, если для некоторых количество хаоса в коде перешло все границы, спешу вас успокоить: в большинстве случаев оперировать «кривыми» цифрами не придётся. Скорее всего в вашем чанке будет намешено столько карт, шумов и градиентов, что они даже против вашей воли внесут необходимый для генерации хаос. Вручную это придётся делать только там, где ландшафт будет плавно переходить в какие-то ровные поверхности, как это было на примере выше. Но это будут единичные случаи.
Итак, мы рассмотрели простейшие примеры смешивания шумов и градиентов, использования карт и т.д. Даже успели увидеть некоторые глюки и узнали, как с ними бороться. Теперь давайте поговорим о недостатках такого подхода. И основной из них – детализация.
Проблема детализации
Конечно же нам всем хочется получить красивый и интересный результат. Порой, для достижения этой цели необходимо сгенерировать что-то поменьше сетки чанка (4х4х8 блоков). Да, с этим хорошо справляются генераторы фич (Features). Они работают не с сеткой, а с самими блоками, но это требует больше ресурсов, и происходит не так быстро, как генерация «сырого» чанка.И да, можно психануть, и уменьшить сетку чанка до размера в один блок, но при этом количество вычислений вырастет в разы, а если быть точным, в 4 х 4 х 8 = 128 раз. Нам бы этого не хотелось.
Чтобы чётче понять проблему детализации, давайте рассмотрим простой пример. Предположим, что мы ходим сгенерировать под землёй узкую пещеру, как на скриншоте.
Здесь серым показан камень, а белым – воздух самой пещеры.
Допустим, что мы какими-то сложными вычислениями расставили по нужным местам необходимые нам веса сетки чанка. Красные – положительные, синие – отрицательные.
Вроде, всё выглядит правильно, и пещера должна получится отличной! Но не забывайте, что финальный ландшафт будет рассчитываться путём интерполяции.
Как наша пещера выглядит для генератора? Примерно вот так. Тёмное – положительное, светлое – отрицательное.
По итогу, после расставления всех блоков, мы получим следующий результат.
Это не сильно напоминает пещеру.
Из ванильного кода видно, что с данной проблемой столкнулись и разработчики игры. Но не зря же они целый год (по их словам) писали свой генератор. В итоге, они придумали довольно интересное решение: если нельзя получить детальный ландшафт на одном «интерполируемом пространстве», значит нужно добавить к нему второе.
Интерполируемые пространства
Что я имею ввиду под интерполируемым пространством? Я имею ввиду всю сетку чанка, с которой в данный момент происходит работа. То есть набор точек, хранящийся в памяти, в результате интерполяции которых мы получаем финальные веса блоков.Что будет, если создать ещё одно подобное пространство? Для каждого конкретного блока в финале мы получим не один, а два веса. Или три. Всё зависит от количества добавляемых пространств. На самом деле, в ванильном генераторе их можно создавать сколько угодно, подобно слоям в фотошопе.
Да, к такому нас жизнь не готовила
И если реально рассматривать трёхмерные шумы как четырёхмерный объект, то с добавлением новых пространств, мы уходим чуть ли не в пятое измерение. Свихнуться можно.
Но, если понять основные принципы и законы построения, это перестанет быть настолько пугающим.
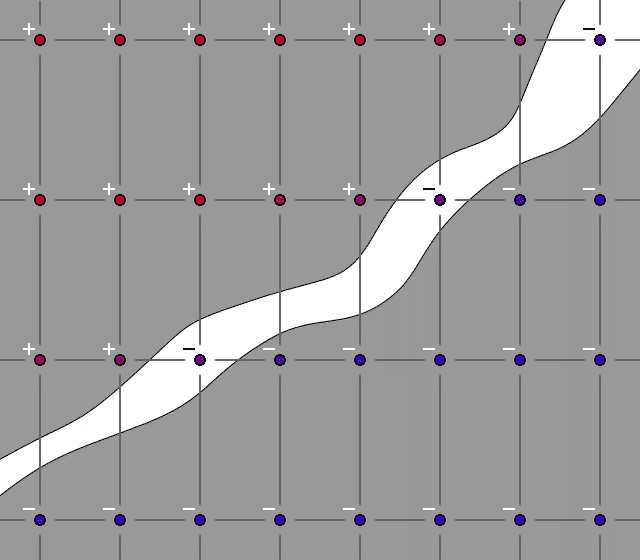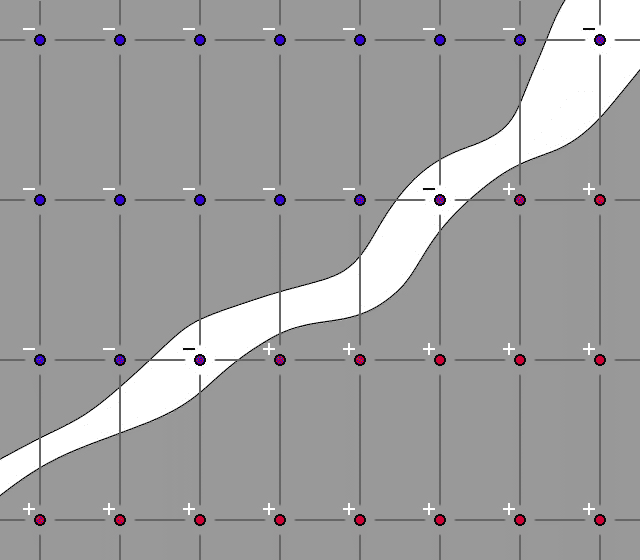
Теперь давайте по порядку. Вернёмся к нашей пещере, но будем использовать не одно, а два пространства. Распределим веса в этих пространствах следующим образом. На первом пространстве все положительные значения будут располагаться с одной стороны пещеры, а на втором – с другой. При этом нужно следить, чтобы на обоих пространствах внутри пещеры веса сохраняли отрицательные значения. Выглядеть это будет примерно так.
После интерполяции получим следующую картину.
В финале, в каждом блоке мы имеем по два веса. При этом, внутри пещеры оба эти веса отрицательные. Теперь нам остаётся только поставить блоки там, где хотя бы один из весов положительный. Если разговаривать языком формул, то выглядеть это будет так:
Java:
double finalWeight = Math.max(weight1, weight2);Ну а финальная картина будет такой.
Таким образом мы получили особенность ландшафта, которая меньше сетки чанка. Количество вычислений при этом увеличилось всего в 2 раза.
Да, конечно, мы видим, что финальная пещера не в точности повторяет наши хотелки, она более сглаженная и не такая интересная. Но мы всегда можем смешать её с ещё одним шумом, чтобы получить некоторые флуктуации.
Для тех, кто не собирается писать свой генератор, а статью читает из чистого любопытства, думаю, приведённая ниже информация будет не очень интересна.
Для всех остальных, я попытаюсь вкратце описать техническую сторону работы с несколькими интерполируемыми пространствами, и тот механизм, который явили миру создатели версии 1.18. Советую читать следующий текст открыв код игры, чтобы была возможность видеть всю картину целиком.
В версии 1.18 появилось несколько интересных классов и интерфейсов:
Все эти элементы вместе образуют довольно мощную и удобную машинку, позволяющую гибко управлять формой ландшафта.
Но давайте по порядку. Разберёмся как же всё это работает. Для того, чтобы собрать все элементы воедино, существует класс
В конструкторе данного класса создаются экземпляры
Метод
При этом сам
Да, ваши глаза вас не обманули: объект (
Метод
Давайте пройдёмся по ней ещё раз, чтобы не запутаться: при создании экземпляра
Но пока что это лишь мёртвые функции. Оживать они начинают позже, в том самом методе
Приведу почти полный код метода, лишь слегка сократив его, вырезав всё лишнее, мешающее восприятию картины.
Таким образом, мы просчитываем веса в точках сетки только один раз для каждой ячейки, но интерполируем их для каждого блока внутри этой ячейки.
Надеюсь, теперь вы достигли такого же просветления, как и я Но вернёмся к основам.
Но вернёмся к основам.
Для всех остальных, я попытаюсь вкратце описать техническую сторону работы с несколькими интерполируемыми пространствами, и тот механизм, который явили миру создатели версии 1.18. Советую читать следующий текст открыв код игры, чтобы была возможность видеть всю картину целиком.
В версии 1.18 появилось несколько интересных классов и интерфейсов:
BlockStateFiller - Заполнитель блоками. Основной функциональный интерфейс, с которым работает генератор. Принимает три значения координат блока и возвращает состояние блока, которое будет размещено в чанке. Это то место, где в наших примерах мы работали с интерполированными весами.NoiseFiller – Заполнитель шумами (или весами). Основной функциональный интерфейс, применяющийся для вычисления веса точек решётки чанка. Принимает три значения координат (в формате координат блока) и возвращает вес точки.NoiseChunk – объект, где хранится основная информация о генерируемом чанке, общие настройки мира, высоты, ширины, размера решётки чанка и т.д., включая необходимые для конкретного чанка 2D карты (континентальность, эрозия и т.д.) и список интерполяторов. Всё это создаётся один раз, сохраняется в памяти и используется на различных этапах генерации данного чанка.Sampler – функциональный интерфейс, единственная задача которого возвращать вес блока.
Java:
@FunctionalInterface
public interface Sampler {
double sample();
}InterpolatableNoise – промежуточный функциональный интерфейс, применяющийся исключительно для создания самплера. Принимает объект NoiseChunk и возвращает Sampler.
Java:
@FunctionalInterface
public interface InterpolatableNoise {
Sampler instantiate(NoiseChunk noiseChunk);
}NoiseInterpolator – самый интересный элемент во всей этой схеме. Интерполятор весов сетки чанка. Является реализацией самплера, то есть способен возвращать интерполированный вес блока. На самом деле, это и есть то самое интерполируемое пространство, в котором происходит вся магия. А именно, это то место, где из набора вершин сетки чанка получают вес каждого конкретного блока.Все эти элементы вместе образуют довольно мощную и удобную машинку, позволяющую гибко управлять формой ландшафта.
Но давайте по порядку. Разберёмся как же всё это работает. Для того, чтобы собрать все элементы воедино, существует класс
NoiseSampler. В нём происходит основной акт творчества и управление всеми описанными выше функциями.В конструкторе данного класса создаются экземпляры
InterpolatableNoise, которые в последующем вернут нам необходимые экземпляры интерполяторов NoiseInterpolator:
Java:
InterpolatableNoise baseNoise;
this.baseNoise = noiseChunk -> noiseChunk.createNoiseInterpolator((x, y, z) -> this.getBaseWeight(x, y, z));createNoiseInterpolator() принимает NoiseFiller и возвращает NoiseInterpolator, одновременно добавляя его в список интерполяторов, хранящийся в экземпляре NoiseChunk-а.При этом сам
NoiseFiller сохраняется в NoiseInterpolator-е и на его основе потом будет генерироваться вес точек чанка.Да, ваши глаза вас не обманули: объект (
NoiseInterpolator) создаётся с помощью одной функции (InterpolatableNoise) и одновременно сохраняет в себе другую (NoiseFiller). Зачем так сделано? Затем, что на моменте создания класса NoiseSampler мы не знаем с какими именно объектами NoiseChunk мы будем работать. Всё это указывается уже на моменте генерации чанка при создании функции BlockStateFiller-а.
Java:
protected BlockStateFiller makeBaseNoiseFiller(NoiseChunk noiseChunk, ...) {
Sampler base = this.baseNoise.instantiate(noiseChunk); // Получение экземпляра интерполятора, который мы уже описали при создании класса NoiseSampler
... // и других необходимых интерполяторов
return (x, y, z) -> { // Создание экземпляра BlockStateFiller-а
double weight = base.sample(); // Получение веса для конкретного блока
... // Получение других интерполированных весов и работа с ними
return noiseChunk.aquifer().computeSubstance(x, y, z, weight); // Определение блока исходя из веса
};
}makeBaseNoiseFiller() вызывается в конструкторе NoiseChunk-а, и по итогу его применения получается своеобразная матрёшка из функций.Давайте пройдёмся по ней ещё раз, чтобы не запутаться: при создании экземпляра
NoiseChunk-а мы получаем сам этот экземпляр, функцию BlockStateFiller-а и включённый в неё список интерполяторов NoiseInterpolator, в каждом из которых хранится свой экземпляр NoiseFiller-а, который и будет создавать веса для интерполяции.Но пока что это лишь мёртвые функции. Оживать они начинают позже, в том самом методе
doFill() генератора чанков. Я же обещал, что мы к нему ещё вернёмся. Сейчас вы поймёте, как авторам удалось сократить количество вычислений при том, что функция нашего BlockStateFiller-а применяется к каждому блоку.Приведу почти полный код метода, лишь слегка сократив его, вырезав всё лишнее, мешающее восприятию картины.
Java:
private ChunkAccess doFill(Blender blender, StructureFeatureManager str, ChunkAccess chunk, int minCellY, int cellCountY) {
NoiseChunk noiseChunk = chunk.getOrCreateNoiseChunk(...); // Создание NoiseChunk-а и всей описанной выше функциональной матрёшки
ChunkPos chunkPos = chunk.getPos();
int minX = chunkPos.getMinBlockX(); // Минимальная X чанка
int minZ = chunkPos.getMinBlockZ(); // Минимальная Z чанка
noiseChunk.initializeForFirstCellX(); // Инициализация первого набора колонн в сетки чанка во всех имеющихся интерполяторах (см. первую статью). В данном методе пробегаются по всему списку интерполяторов и запускают у них NoiseFiller-ы, заполняя точки сетки значениями весов.
int cellWidth = this.settings.get().noiseSettings().getCellWidth(); // Ширина яцейки в сетки чанка
int cellHeight = this.settings.get().noiseSettings().getCellHeight(); // Высота яцейки в сетки чанка
int cellCountX = 16 / cellWidth; // Количество ячеек в чанке по X
int cellCountZ = 16 / cellWidth; // Количество ячеек в чанке по Y
for (int xCell = 0; xCell < cellCountX; ++xCell) { // Пробегаемся по всем ячейкам в чанке по X
noiseChunk.advanceCellX(xCell); // Инициализируем следующий набор колонн. Их у нас уже два.
for (int zCell = 0; zCell < cellCountZ; ++zCell) { // Пробегаемся по всем ячейкам в чанке по Z
LevelChunkSection section = chunk.getSection(chunk.getSectionsCount() - 1); // Берём секцию чанка 16х16х16, которую будем заполнять блоками
for (int yCell = cellCountY - 1; yCell >= 0; --yCell) { // Пробегаемся по всем ячейкам в чанке по Y
noiseChunk.selectCellYZ(yCell, zCell); // Берём все точки в текущей ячейке (8 штук), которые будем интерполировать
// Далее работаем уже внутри ячейки непосредственно с блоками
for (int yLocal = cellHeight - 1; yLocal >= 0; --yLocal) { // Пробегаемся по всем блокам внутри
int y = (minCellY + yCell) * cellHeight + yLocal; // Выясняем координату Y блока в мире
int ySection = y & 15; // И её же внутри секции чанка
int indexSection = chunk.getSectionIndex(y); // Индекс секции
if (chunk.getSectionIndex(section.bottomBlockY()) != indexSection) { // Если мы опустились ниже текущей секции, берём следующую
section = chunk.getSection(indexSection);
}
double deltaY = (double) yLocal / (double) cellHeight; // Выясняем пропорциональное размещение блока внутри ячейки
noiseChunk.updateForY(deltaY); // Пробегаемся по всем интерполяторам и интерполируем точки ячейки попарно по оси Y. Из 8-ми точек получаем 4.
for (int xLocal = 0; xLocal < cellWidth; ++xLocal) {
int x = minX + xCell * cellWidth + xLocal;
int xSection = x & 15;
double deltaX = (double) xLocal / (double) cellWidth;
noiseChunk.updateForX(deltaX); // Повторяем интерполяцию для координаты X. Остаётся уже 2 точки.
for (int zLocal = 0; zLocal < cellWidth; ++zLocal) {
int z = minZ + zCell * cellWidth + zLocal;
int zSection = z & 15;
double deltaZ = (double) zLocal / (double) cellWidth;
noiseChunk.updateForZ(deltaZ); // Делаем то же самое для оси Z. В итоге получаем интерполированный вес блока в каждом из интерполяторов, то есть для каждого интерполируемого пространства.
BlockState blockstate = this.materialRule.apply(noiseChunk, x, y, z); // В даном месте мы имеем экземпляр NoiseChunk-а с финальными весами и можем запускать наш BlockStateFiller, чтобы помять их так, как нам надо, и определить финальное состояние блока
if (blockstate == null) blockstate = this.defaultBlock;
if (blockstate != AIR) section.setBlockState(x, y, z, blockstate, false); // Размещаем блок в секции чанка
}
}
}
}
}
noiseChunk.swapSlices(); // После прохождения всех ячеек внутри первых двух наборов колонн, удаляем первый набор, а второй копируем в первый (см. первую статью). На месте второго набора на следующем этапе цикла будут размещены новые веса точек.
}
return chunk;
}Надеюсь, теперь вы достигли такого же просветления, как и я
Играясь с несколькими интерполируемыми пространствами, мы реально можем лепить из ландшафта то, что нам хочется. Главное, это разработать алгоритм получения той или иной формы. И это опять зависит только от вас и вашей фантазии. Я же, со своей стороны, могу лишь привести ещё один пример элегантного решения, и примером этим будут: ванильные лапшичные пещеры.
Лапшичные пещеры
Внимательный читатель мог заметить ошибку в описании пространственного построения предыдущей пещеры. Дело в том, что в качестве примера я для наглядности использовал двухмерное сечение чанка, на котором ясно было видно с какой из сторон пещеры на каждом из пространств располагаются положительные веса. Но ведь пещера – это трёхмерный объект, и нам не всегда будет понятно, где у неё какая сторона.Как говорила Алиса: «С одной стороны чего? И с другой стороны чего?!»
На самом деле, если бы мы сгенерировали приведённый мною пример, то получили бы вовсе не пещеру, а широченный наклонный холл с низким потолком. На одном из пространств положительные веса располагались бы над этим холлом, а на втором – под ним.
Чтобы ограничить его и по ширине, пришлось бы использовать ещё два пространства. Это усложнило бы процесс. Но есть способ хитрее: ванильный генератор предполагает разделение сложных и не сложных вычислений. К примеру, вычисление веса какой-либо из точек чанка может быть довольно сложным, так как оно завязано на положение этой точки в пространстве, сочетание различных шумов, градиентов и их преобразованиях. С другой стороны, выяснение ставить ли блок на месте положительного веса происходит очень даже легко. Там всего одно условие.
Как вы догадались, сложные вычисления выполняются только для точек решётки чанка, а простые мы можем себе позволить считать для каждого блока.
Ну и раз уж они такие простые, так почему бы и не добавить к ним ещё несколько несложных преобразований? Например, таких:
Java:
double finalWeight = Math.abs(weight) - 0.5;Эту:
Что-то похожее мы уже видели, правда?
Да, как вы догадались, я сформировал узкую пещеру (в вертикальном сечении) на основе единственного интерполируемого пространства, лишь слегка поработав с финальным весом блока. Второе же пространство можно использовать для ограничения этой пещеры по ширине, то есть в горизонтальном сечении.
Как это получилось?
Следующие схемы в полной мере ответят на данный вопрос.
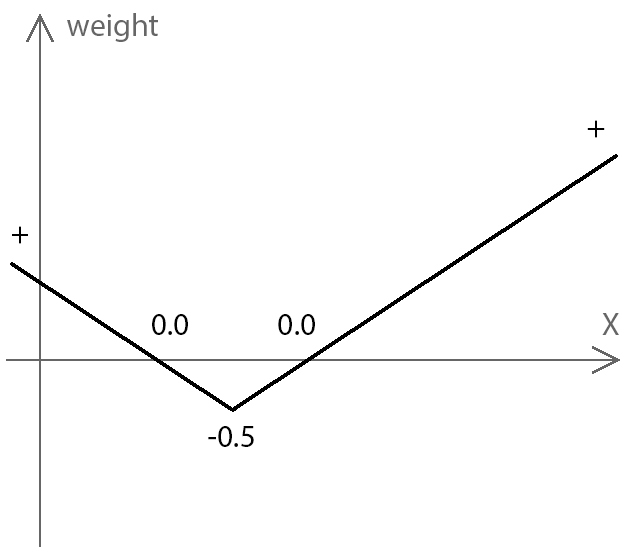
На предыдущих картинках я показывал сечение чанка, чтобы градиент весов или трёхмерный шум можно было увидеть нашим двухмерным зрением. Теперь пойдём ещё дальше и сделаем сечение по сечению, представим градиент в виде графика
x – weight.Теперь вычислим модуль градиента, то есть все отрицательные значения сделаем положительными. Иными словами, отзеркалим график относительно нулевой отметки.
Ну и следующий шаг: опустим график на
0.5.Таким образом, в месте, где градиент пересекал нулевую отметку, мы получили узкую полоску отрицательных значение. Всё остальное поле стало положительным.
Думаю, теперь вам стал понятен смыл описанной выше формулы.
Ну а сейчас настало время включить на полную своё пространственное воображение и погрузиться с головой в создание «лапшичных» пещер. На этот раз работать мы будем не с градиентом, а с трёхмерным шумом, но над ним мы будем производить примерно те же манипуляции, что были описаны ранее.
Помните, в первой статье я показывал скриншот генерации, на основе чистого шума значений? Ландшафт на нём напоминал трёхмерную губку. Её форма в точности повторяла поверхность нулевых значений в шуме. Ровно таких же нулевых значений, с которыми мы уже работали в примере с градиентом. Это значит, что и к интерполированным значениям трёхмерного шума можно применить ту же самую формулу, что мы применяли к градиенту. Но результатом будет не низкий и широкий холл, а кое-что гораздо более сложное. У нулевой поверхности шума появится толщина! Изнутри это будет выглядеть примерно так.
Если вы способны понять, что здесь происходит, браво! Значит я не зря писал эту статью.
Если это всё-таки трудновато, то вот вам сечение по шуму и результат применения формулы.
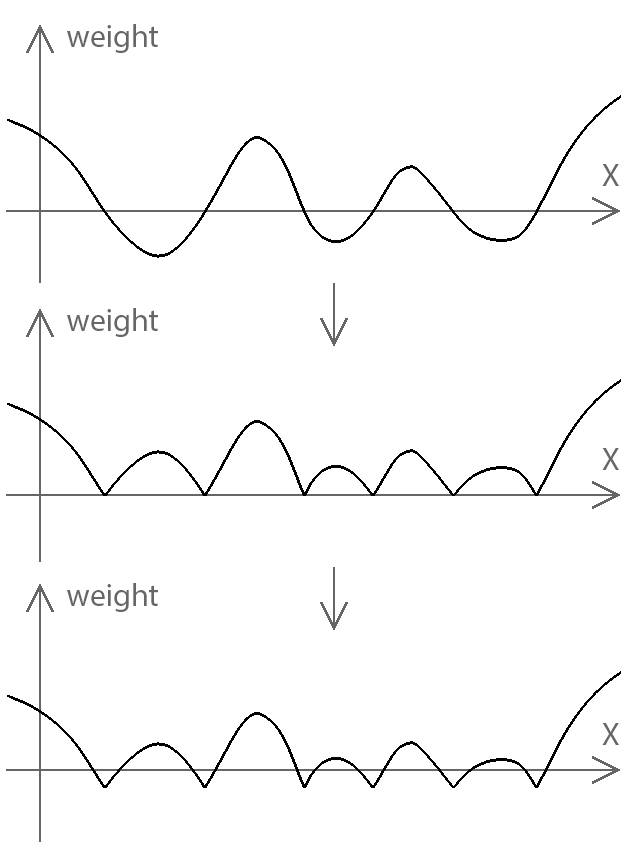
Ну а если всё ещё не понятно, то вот вам и сечение по сечению шума и последовательность его преобразований.
Так уже понятнее, правда? Но, уверяю вас, это ещё не самое страшное. Здесь мы получили только одно интерполируемое пространство, которое, подобно примеру с градиентом, ограничивает наши будущие пещеры только с двух сторон, «сверху» и «снизу». Если такие понятия вообще применимы к предыдущему скриншоту. Теперь нам нужно добавить сюда ещё одно пространство с шумом. Только второй шум должен чем-то отличаться от первого, например размером или сидом.
Что происходит далее? Правильно! Мы пересекаем одно пространство со вторым так, как это делали ранее, используя формулу:
Java:
double finalWeight = Math.max(weight1, weight2);Ах да! В середине статьи я упоминал, что для создания лапшичных пещер используются четыре шума. Два из них я описал, а ещё два выполняют функцию деформирования. По первому шуму определяют толщину пещеры, то есть то число, которое вычитается из модуля весов. Второй же шум определяет само место размещения данных пещер, чтобы они встречались не во всём подземном мире, а лишь в некоторых местах (смотри самый первый пример с использованием шума, в качестве карты).
В коде игры это выглядит так:
Java:
protected NoiseChunk.BlockStateFiller makeBaseNoiseFiller(NoiseChunk noiseChunk, NoiseChunk.NoiseFiller filler, boolean generaneNoodle) {
NoiseChunk.Sampler base = this.baseNoise.instantiate(noiseChunk); // Инициализация интерполятора базовых весов чанка (в наших примерах это был чистый градиент)
NoiseChunk.Sampler toggle = generaneNoodle ? this.noodleToggle.instantiate(noiseChunk) : () -> -1.0D; // Инициализация интерполятора распределения пещер
NoiseChunk.Sampler thickness = generaneNoodle ? this.noodleThickness.instantiate(noiseChunk) : () -> 0.0D; // Инициализация интерполятора толщины пещер
NoiseChunk.Sampler ridgeA = generaneNoodle ? this.noodleRidgeA.instantiate(noiseChunk) : () -> 0.0D; // Инициализация интерполятора шума №1
NoiseChunk.Sampler ridgeB = generaneNoodle ? this.noodleRidgeB.instantiate(noiseChunk) : () -> 0.0D; // Инициализация интерполятора шума №2
return (x, y, z) -> {
double weight = base.sample(); // Достаём базовый вес
double finalWeight = Mth.clamp(weight * 0.64D, -1.0D, 1.0D);
finalWeight = finalWeight / 2.0D - finalWeight * finalWeight * finalWeight / 24.0D; // Производим над базовым весом кое-какие оптимизации
if (toggle.sample() >= 0.0D) { // Выясненяем, будет ли в этом месте вообще хоть что-то генерироваться (вспоминаем первый пример)
double minThickness = 0.05D;
double maxThickness = 0.1D;
double finalFhickness = Mth.clampedMap(thickness.sample(), -1.0D, 1.0D, minThickness, maxThickness); // Определяем толщину пещеры
double noise1 = Math.abs(1.5D * ridgeA.sample()) - finalFhickness; // Манипуляции с первым шумом (см. формулу из примера)
double noise2 = Math.abs(1.5D * ridgeB.sample()) - finalFhickness; // Манипуляции со вторым шумом (см. формулу из примера)
finalWeight = Math.min(finalWeight, Math.max(noise1, noise2)); // Наша знакомая формула, но немного переработанная
}
finalWeight += filler.calculateNoise(x, y, z); // Для веселья смешиваем получившийся вес с шумом ландшафта
return noiseChunk.aquifer().computeSubstance(x, y, z, weight, finalWeight); // Определяем финальное состояние блока с использованием аквифера (об этом речь пойдёт в следующей статье)
};
}Напоследок, вот вам несколько скриншотов из Туманного мира

А то я боялся, что очень затянуто получилось.